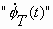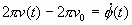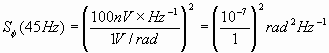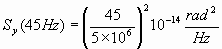VIII. SPECTRUM ANALYSIS

Another method of characterizing the noise in a signal source is by means of spectrum analysis. To understand this approach, let's examine the waveform shown in figure 8.1.

Here we have a sine wave which is perturbed for short instances by noise. Some loosely refer to these types of noises as "glitches". The waveform has a nominal frequency over one cycle which we'll call "n ₀" (n ₀ = 1/T). At times, noise causes the instantaneous frequency to differ markedly from the nominal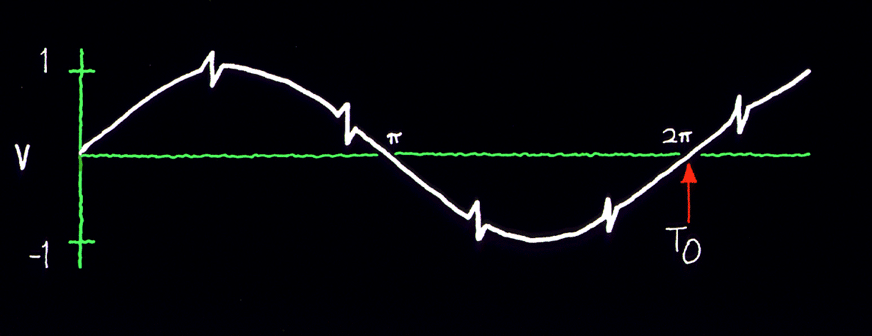

Figure 8.1: Sine wave that is perturbed by periodic glitches.

frequency. If a pure sine wave signal of frequency n ₀ is subtracted from this waveform, the remainder is the sum of the noise component. These components are of a variety of frequencies and the sum of their amplitudes is nearly zero except for the intervals during each glitch when their amplitudes momentarily reinforce each other. This is shown graphically in figure 8.2.

One can plot a graph showing rms power vs. frequency for a given signal. This kind of plot is called the power spectrum. For the waveform of figure 8.1 the power spectrum will have a high value at n ₀ and will have lower values for the signals produced by the glitches. Closer analysis reveals that there is a recognizable, somewhat constant repetition rate associated with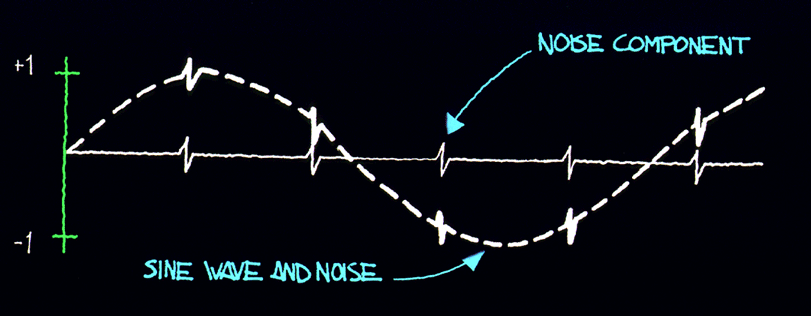

Figure 8.2: Periodic glitches are undesirable and can be separated from the desired sine wave and characterized in the frequency domain.

the glitches. In fact, we can deduce that there is a significant amount of power in another signal whose period is the period of the glitches as shown in figure 8.2. Let's call the frequency of the glitches n _s. Since this is the case, we will observe a noticeable amount of power in the spectrum at n _s with an amplitude which is related to the characteristics of the glitches. The power spectrum shown in figure 8.3 has this feature. A predominant n _s component has been depicted, but other harmonics also exist.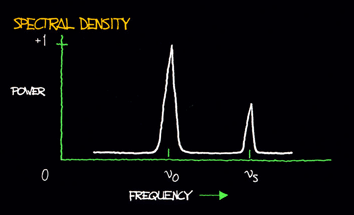

Figure 8.3: A plot of power (into a load) vs. frequency is a power spectrum.

Some noise will cause the instantaneous frequency to "jitter" around n ₀, with probability of being higher or lower than n ₀. We thus usually find a "pedestal" associated with n ₀ as shown in figure 8.4.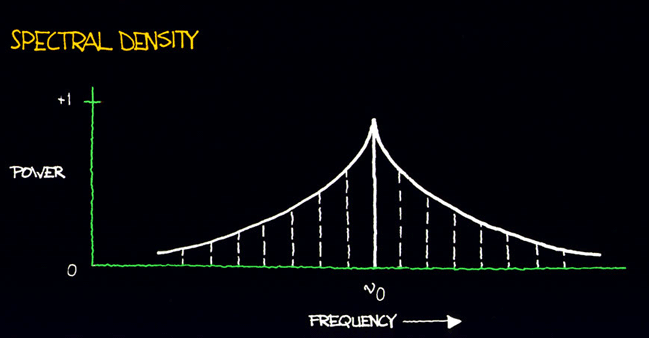

Figure 8.4: The power spectrum of an oscillator includes its “noise pedestal.”

The process of breaking down a signal into all of its various components of frequency is called Fourier expansion (see sec. X). In other words, the addition of all the frequency components, called Fourier frequency components, produces the original signal. The value of a Fourier frequency is the difference between the frequency component and the fundamental frequency. The power spectrum can be normalized to unity such that the total area under the curve equals one. The power spectrum normalized in this way is the power spectral density.

The power spectrum, often called the RF spectrum, of V(t) is very useful in many applications. Unfortunately, if one is given the RF spectrum, it is impossible to determine whether the power at different Fourier frequencies is a result of amplitude fluctuations "a(t)" or phase fluctuations "f (t)." The RF spectrum can be separated into two independent spectra, one being the spectral density of "f (t)".

For the purposes here, the phase-fluctuation components are the ones of interest. The spectral density of phase fluctuations is denoted by Sf (f) where "f" is Fourier frequency. For the frequently encountered case where the AM power spectral density is negligibly small and the total modulation of the phase fluctuations is small (mean-square value is much less than one rad²), the RF spectrum has approximately the same shape as the phase spectral density.

However, a main difference in the representation is that the RF spectrum includes the fundamental signal (carrier), and the phase spectral density does not. Another major difference is that the RF spectrum is a power spectral density and is measured in units of watts/hertz. The phase spectral density involves no "power" measurement of the electrical signal. The units are radians²/hertz. It is tempting to think of Sf (f) as a "power" spectral density because in practice it is measured by passing V(t) through a phase detector and measuring the detector's output power spectrum. The measurement technique makes use of the relation that for small deviations (d f « 1 radian),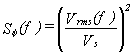

    (8.3)

where V_rms(f) is the root-mean-square noise voltage per Ö Hz at a Fourier frequency "f", and V_s is the sensitivity (volts per radian) at the phase quadrature output of a phase detector which is comparing the two oscillators. In the next section, we will look at a scheme for directly measuring Sf (f).

One question we might ask is, "How do frequency changes relate to phase fluctuations?" After all it's the frequency stability of an oscillator that is a major consideration in many applications. The frequency is equal to a rate of change in the phase of a sine wave. This tells us that fluctuations in an oscillator's output frequency are related to phase fluctuations since we must change the rate of "f (t)" to accomplish a shift in "n (t)", the frequency at time t. A rate of change of total "f _T(t)" is denoted by

We have then

  (8.4)

The dot denotes the mathematical operation of differentiation on the function f _T with respect to its independent variable t. From eq (8.4) and eq (1.1) we get

Rearranging, we have

or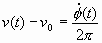

  (8.5)

The quantity n (t) - n ₀ can be more conveniently denoted as d n (t), a change in frequency at time t. Equation (8.5) tells us that if we differentiate the phase fluctuations f (t) and divide by 2p , we will have calculated the frequency fluctuation d n (t). Rather than specifying a frequency fluctuation in terms of shift in frequency, it is useful to denote d n (t) with respect to the nominal frequency n ₀. The quantity d n (t)/n ₀ is called the fractional frequency fluctuation at time t and is signified by the variable y(t). We have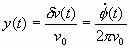

  (8.6)

The fractional frequency fluctuation y(t) is a dimensionless quantity. When talking about frequency stability, its appropriateness becomes clearer if we consider the following example. Suppose in two oscillators d n (t) is consistently equal to + 1 Hz and we have sampled this value for many times t. Are the two oscillators equal in their ability to produce their desired output frequencies? Not if one oscillator is operating at 10 Hz and the other at 10 MHz. In one case, the average value of the fractional frequency fluctuation is 1/10, and in the second is 1/10,000,000 or 1 x 10^-7. The 10 MHz oscillator is then more precise. If frequencies are multiplied or divided using ideal electronics, the fractional stability is not changed.

In the frequency domain, we can measure the spectrum of frequency fluctuations y(t). The spectral density of frequency fluctuations is denoted by S_y(f) and is obtained by passing the signal from an oscillator through an ideal FM detector and performing spectral analysis on the resultant output voltage. S_y(f) has dimensions of (fractional frequency)²/Hz or Hz^-1. Differentiation of f (t) corresponds to multiplication by f/n ₀ in terms of spectral densities. With further calculation, one can derive that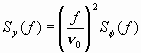

  (8.7)

We will address primarily Sf (f), that is, the spectral density of phase fluctuations. For noise-measurement purposes, Sf (f) can be measured with a straightforward, easily duplicated equipment set-up. Whether one measures phase or frequency spectral densities is of minor importance since they bear a direct relationship. It is important, however, to make the distinction and to use eq (8.7) if necessary.

8.1 The Loose Phase-Locked Loop

Section I, 1.1, C described a method of measuring phase fluctuations between two phase-locked oscillators. Now we will review a common procedure for measuring Sf (f).

Suppose we have a noisy oscillator. We wish to measure the oscillator's phase fluctuations relative to nominal phase. One can do this by phase-locking another oscillator (called the reference oscillator) to the test oscillator and mixing the two oscillator signals 90° out of phase (phase quadrature). This is shown schematically in figure 8.9. The two oscillators are at the same frequency in long term as guaranteed by the phase-lock loop (PLL). A low-pass filter (to filter the R.F. sum component) is used after the mixer since the difference (baseband) signal is the one of interest. By holding the two signals at a relative phase difference of 90° , short-term phase fluctuations between the test and reference oscillators will appear as voltage fluctuations out of the mixer.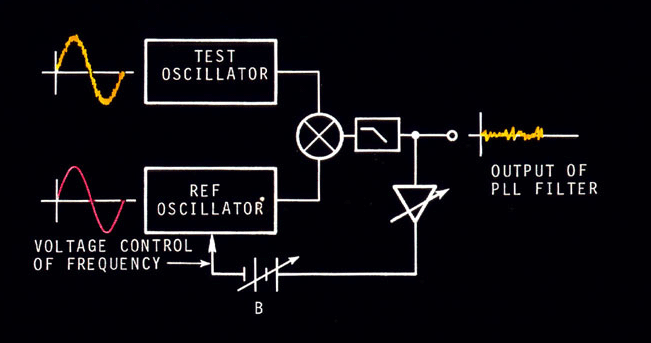

Figure 8.9: The phase noise of a test oscillator is usually measured by a loose phase-locked loop. The test and reference oscillators will naturally lock so that their signals have a phase difference of 90 deg. and the PLL output voltage fluctuations correspond to phase fluctuations between the oscillators.

With a PLL, if we can make the servo time constant very long, then the PLL bandwidth as a filter will be small. This may be done by lowering the gain A_v of the loop amplifier. We want to translate the phase modulation spectrum to baseband spectrum so that it is easily measured on a low frequency spectrum analyzer. With a PLL filter, we must keep in mind that the reference oscillator should be as good or better than the test oscillator. This is because the output of the PLL represents the noise from both oscillators, and if not properly chosen, the reference can have noise masking the noise from the test oscillator. Often, the reference and test oscillators are of the same type and have, therefore, approximately the same noise. We can acquire a meaningful measurement by noting that the noise we measure is from two oscillators. Many times a good approximation is to assume that the noise power is twice that which is associated with one oscillator. Sf (f) is general notation depicting spectral density on a per hertz basis. A PLL filter output necessarily yields noise from two oscillators.

The output of the PLL filter at Fourier frequencies above the loop bandwidth is a voltage representing phase fluctuations between reference and test oscillator. It is necessary to make the time-constant of the loop long compared with the inverse of the lowest Fourier frequency we wish to measure.

That is,

This means that if we want to measure Sf (f) down to 1 Hz, the loop time-constant must be greater than 1/2p seconds. One can measure the time-constant by perturbing the loop (momentarily disconnecting the battery is convenient) and noting the time it takes for the control voltage to reach 70% of its final value. The signal from the mixer can then be inserted into a spectrum analyzer. A preamp may be necessary before the spectrum analyzer.

The analyzer determines the mean square volts that pass through the analyzer's bandwidth centered around a pre-chosen Fourier frequency f. It is desirable to normalize results to a 1 Hz bandwidth. Assuming white phase noise (white PM), this can be done by dividing the mean square voltage by the analyzer bandwidth in Hz. One may have to approximate for other noise processes. (The phase noise sideband levels will usually be indicated in rms volts-per-root-Hertz on most analyzers.)

8.2 Equipment for Frequency Domain Stability Measurements

(1)Low-noise mixer

This should be a high quality, double-balanced type, but single-ended types may be used. The oscillators should have well-buffered outputs to be able to isolate the coupling between the two input RF ports of the mixer. Results that are too good may be obtained if the two oscillators coupel tightly via signal injection through the input ports. We want the PLL to control locking. One should read the specificiations in order to prevent exceeding the maximum allowable input power to the mixer. It is best to operate near the maximum for best signal-to-noise out of the IF port of the mixer and, in some cases, it is possible to drive the mixer into saturation without burning out the device.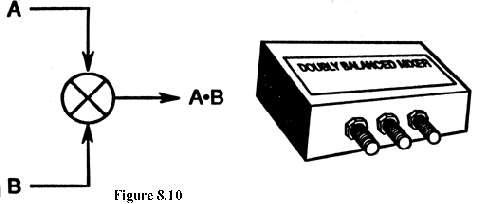

Figure 8.10: A low noise mixer is a key component for precise phase-noise measurements.

(2)Low-noise DC amplifier

The amount of gain A_v needed in the loop amplifier will depend on the amplitude of the mixer output and the degree of varactor control in the reference oscillator. We may need only a small amount of gain to acquire lock. On the other hand, it may be necessary to add as much as 80 dB of gain. Good low-noise DC amplifiers are available from a number of sources, and with cascading stages of amplification, each contributing noise, it will be the noise of the first stage which will add most significantly to the noise being measured. If a suitable low-noise first-stage amplifier is not readily available, a schematic of an amplifier with 40 dB of gain is shown in figure 8.11 which will serve nicely for the first stage. Amplifiers with very low equivalent input noise performance are also available from many manufacturers. The response of the amplifier should be flat from DC to the highest Fourier frequency one wishes to measure. The loop time-constant is inversely related to the gain A_v and the determination of A_v is best made by experimentation knowing that

(3)Voltage-controlled reference quartz oscillator

This oscillator should be a good one with specifications available on its frequency domain stability. The reference should be no worse than the test oscillator. The varactor control should be sufficient to maintain phase-lock of the reference. In general, low quality test oscillators may have varactor control of as much as 1 ´ 10^-6 fractional frequency change per volt. Some provision should be available on the reference oscillator for tuning the mean frequency over a frequency range that will enable phase-lock. Many factors enter into the choice of the reference oscillator, and often it is convenient to simply use two test oscillators phase-locked together. In this way, one can assume that the noise out of the PLL filter is no worse than 3 dB greater than the noise from each oscillator. If it is uncertain that both oscillators are contributing approximately equal noise, then one should perform measurements on three oscillators taking two at a time. The noisier-than-average oscillator will reveal itself.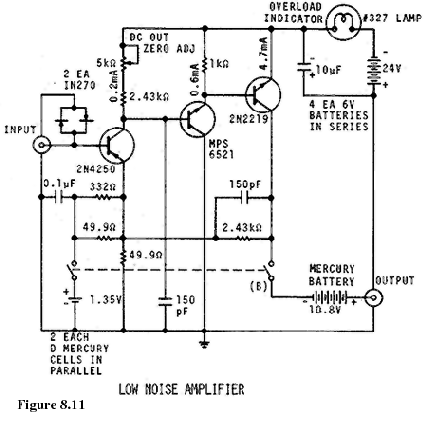

(4)Spectrum analyzer

The signal analyzer typically should be capable of measuring the noise in rms volts in a narrow bandwidth from near 1 Hz to the highest Fourier frequency of interest. This may be 50 kHz for carrier frequencies of 10 MHz or lower. For voltage measuring analyzers, it is typical to use units of "volts per Ö Hz". The spectrum analyzer and any associated input amplifier will exhibit high-frequency rolloff. The Fourier frequency at which the voltage has dropped by 3 dB is the measurement system bandwidth f_h, or w _h = 2p f_h. This can be measured directly with a variable signal generator.

Section X describes how analysis can be performed using a discrete Fourier transform analyzer. Lowering costs of digital technology have made the use of fast-fourier transform analysis affordable.

Rather than measure the spectral density of phase fluctuations between two oscillators, it is possible to measure the phase fluctuations introduced by a device such as an active filter or amplifier. Only a slight modification of the existing PLL filter equipment set up is needed. The scheme is shown in figure 8.12.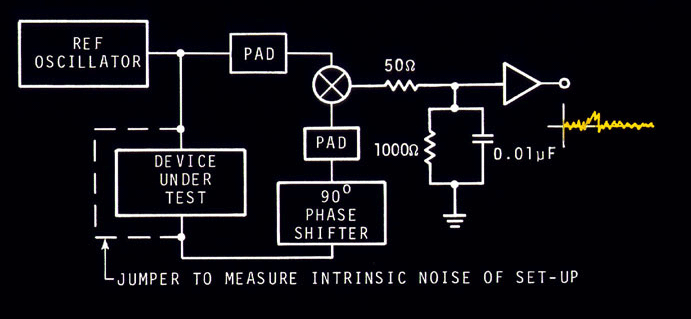

Figure 8.12: The measurement of the noise floor of the measurement system requires a 90 deg. phase shifter.

Figure 8.12 is a differential phase noise measurement set-up. The output of the reference oscillator is split so that part of the signal passes through the device under test. We want the two signals going to the mixer to be 90° out of phase, thus, phase fluctuations between the two input ports cause voltage fluctuations at the output. The voltage fluctuations then can be measured at various Fourier frequencies on a spectrum analyzer.

To estimate the noise inherent in the test set-up, one can in principle bypass the device under test and compensate for any change in amplitude and phase at the mixer. The PLL filter technique must be converted to a differential phase noise technique in order to measure inherent test equipment noise. It is a good practice to measure the system noise before proceeding to measurement of device noise.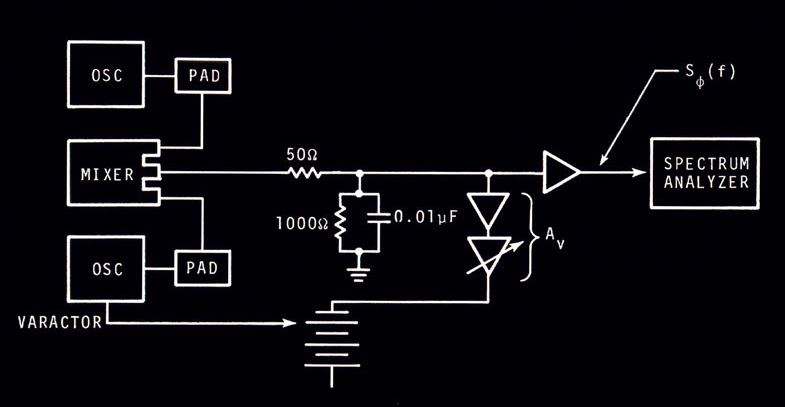

A frequency domain measurement set-up is shown schematically in figure 8.13. The component values for the low-pass filter out of the mixer are suitable for oscillators operating at around 5 MHz.

Figure 8.13: Typical hookup for a phase-noise measurement using a loose PLL.

The active gain element (A_v) of the loop is a DC amplifier with flat frequency response. One may replace this element by an integrator to achieve high gain near DC and hence, maintain better lock of the reference oscillator in long term. Otherwise long-term drift between the reference and test oscillators might require manual re-adjustment of the frequency of one or the other oscillator.⁵

8.3 Procedure and Example

At the input to the spectrum analyzer, the voltage varies as the phase fluctuations in short-term

V_s is the phase sensitivity of the mixer in volts per radian. Using the previously described equipment set-up, V_s can be measured by disconnecting the feedback loop to the varactor of the reference oscillator. The peak voltage swing is equal to V_s in units of volts/rad if the resultant beat note is a sine wave. This may not be the case for state-of-the-art Sf (f) measurements where one must drive the mixer very hard to achieve low mixer noise levels. Hence, the output will not be a sine wave, and the volts/rad sensitivity must be estimated by the slew-rate (through zero volts) of the resultant square-wave out of the mixer/amplifier.

The value for the measured Sf (f) in decibels is given by:

EXAMPLE: Given a PLL with two oscillators such that, at the mixer output:

V_s = 1 volt/rad

V_rms(45 Hz) = 100 nV per root hertz. Solve for Sf (45 Hz).

In decibels,

= 20 (-7) = -140 dB at 45 Hz.

In the example, note that the mean frequency of the oscillators in the PLL was not essential to computing Sf (f). However, in the application of Sf (f), the mean frequency n ₀ is necessary information. Along with Sf (f), one should always refer to n ₀. In the example above n ₀ = 5 MHz, we have

From eq (8.7), S_y(f) can be computed as

S_y(45 Hz) = 8.1 ´ 10^-25 Hz^-1, n ₀ = 5 MHz.

Main Page Table of Contents

Go to section:

Summary and Introduction I II III IV V VI VII VIII IX X XI XII Conclusion References