IX. POWER-LAW NOISE PROCESSES

Power-law noise processes are models of precision oscillator noise that produce a particular slope on a spectral density plot. We often classify these noise processes into one of five categories. For plots of Sf (f), they are:

1.Random walk FM (random walk of frequency), Sf plot goes down as 1/f⁴.

2.Flicker FM (flicker of frequency), Sf plot goes down as 1/f³.

3.White FM (white of frequency), Sf plot goes down as 1/f².

4.Flicker PM (flicker of phase), Sf plot goes down as 1/f.

5.White PM (white of phase), Sf plot is flat.

Power law noise processes are characterized by their functional dependence on Fourier frequency. Equation 8.7 relates Sf (f) to S_y(f), the spectral density of frequency fluctuations. Translation of S_y(f) to time-domain data s _y(t ) for the five model noise processes is covered later in section XI.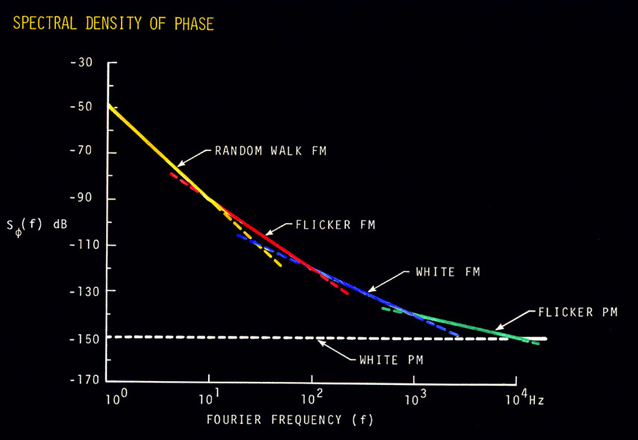

Figure 9.1: Power-law noise is indicated by a particular slope in the phase-noise measurement.

The spectral density plot of a typical oscillator's output usually is a combination of different power-law noise processes. It is very useful and meaningful to categorize the noise processes. The first job in evaluating a spectral density plot is to determine which type of noise exists for a particular range of Fourier frequencies. It is possible to have all five noise processes being generated from a single oscillator, but, in general, only two or three noise processes are dominant. Figure 9.1 is a graph of Sf (f) showing the five noise processes on a log-log scale.

Figure 9.2 shows the spectral density of phase fluctuations for a typical high-quality oscillator.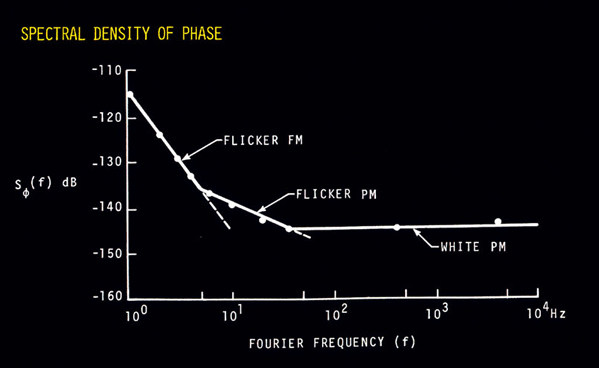

Figure 9.2: Different power-law noises have different causes in an oscillators output signal.

Main Page Table of Contents

Go to section:

Summary and Introduction I II III IV V VI VII VIII IX X XI XII Conclusion References