|
|
|
|
|
Time Domain Stability Statistics
|
|
|
|
|
Thêo1 is in a new class of statistics which mimic the properties of the Allan variance (AVAR) while covering a larger range of averaging times, 10 to N-2 for Thêo1 vs. 1 to (N-1)/2 for AVAR. For averaging times that are common to both, Thêo1 has the same expected value as the Allan variance if bias is removed. It is useful to combine a bias-removed version of Thêo1, called ThêoBR, with AVAR to produce a composite stability plot. The composite is called "ThêoH" which is short for "hybrid-ThêoBR."
ThêoBR is an improved bias-removed version of Thêo1 given by

ThêoBR can determine an unbiased estimate of the Allan variance over the widest possible range of averaging times without explicit knowledge of the noise type. However, ThêoBR in the equation above is computationally intensive for large data sets. Computation time can be significantly reduced by phase averaging with negligible effect on bias removal. For example, a data set of 1,000 points can be divided into ten sets of 100 points. Each set of 100 points can be averaged, and a new data set of ten points represents the original set of 1,000 points. This technique dramatically reduces computation time on a typical desktop computer for large data sets of 10,000 points or more.
ThêoH is a hybrid statistic that combines ThêoBR and AVAR:
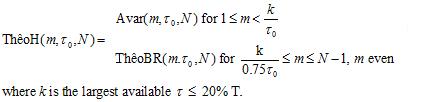
ThêoH is the best statistic available for estimating the stability of a frequency source at large averaging factors.
ThêoH is ideal for determining frequency stability when the data run is of limited duration. An example of a ThêoH applied to data from a laser frequency that is locked to a stable optical cavity is shown in the figure below: The figures show the raw frequency data (above) and the frequency stability (below) of a free-running 563 nm laser ultimately locked to a mechanically stable optical cavity.
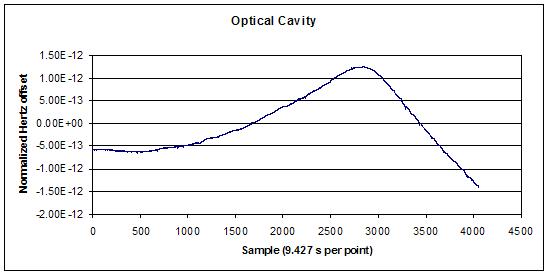
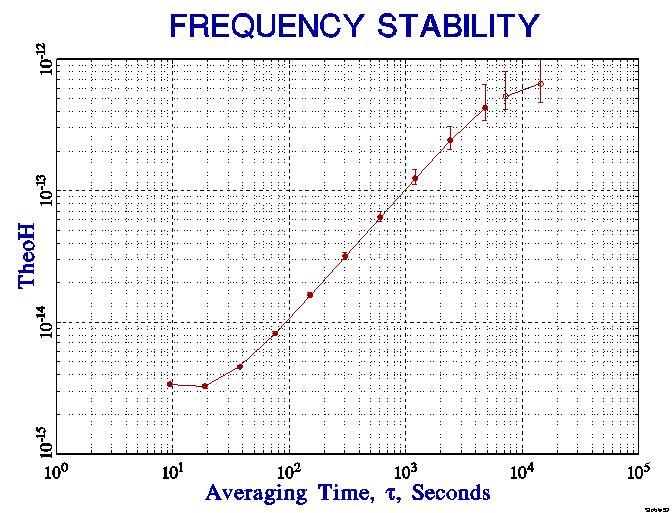
Data courtesy of J. Bergquist and S. Diddams, NIST, June 2006.
We see that ThêoH is a composite of AVAR on the left plot (solid dots) and ThêoBR on the right (circles). The presence of steep τ+1 slope in short-term might be interpreted as frequency drift; however, systematic drift is not indicated in the raw frequency data. By using ThêoH, we can see a long-term slope change towards apparent RWFM whose level can be estimated, even for this limited data run.
References:
1. D.A. Howe and T.K. Peppler, "Very Long-Term Frequency Stability: Estimation Using a Special-Purpose Statistic," Proceedings of the 2003 IEEE International Frequency Control Symposium, pp. 233-238, May 2003.
2. D.A. Howe and T.N. Tasset, "Thêo1: Characterization of Very Long-Term Frequency Stability," Proc. 2004 EFTF.
3. D.A. Howe, "ThêoH: A Hybrid, High-Confidence Statistic that Improves on the Allan Deviation," Metrologia 43 (2006), S322-S331.
4. J. McGee and D.A. Howe, "Fast TheoBR: A method for long data set stability analysis", IEEE Trans. Ultrasonics, Ferroelectrics and Freq. Contrl., to be published, 2008.
5. J. McGee and D.A. Howe, "ThêoH and Allan Deviation as Power-Law Noise Estimators," IEEE Trans. Ultrasonics, Ferroelectrics and Freq. Contrl., Feb. 2007.
