Nuclear quadrupole resonances (NQRs) have persistent relevance in the field of precision measurements and are generating renewed interest for applications of remote sensing– particularly in the case of explosives detection. NQR resonances are also relevant to the application of building better rotation sensors based on nuclear magnetic resonance (NMR), since NQR interactions cause frequency shifts that complicate the realization of such sensors.

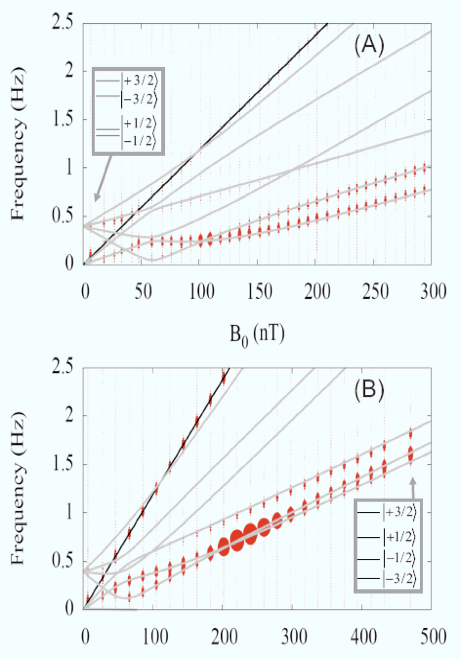
Figure 1: Spectra versus applied field for ϕ = 22° (A) and ϕ = 39° (B). Each vertical line represents a different frequency spectrum acquired at the specific magnetic field that it intersects on the horizontal axis. The symbol size is proportional to the signal amplitude, and the same amplitude scale was used for both angles of ϕ. The inset in (A) shows the 131Xe nuclear energy levels in the low-field NQR regime. The |±3/2 states are degenerate at zero field, as are the |±1/2 states. The inset in (B) shows the nuclear energy levels in the high-field NMR regime.

We have experimentally mapped the transformation of nuclear quadrupole resonances from the pure nuclear quadrupole regime to the quadrupole-perturbed Zeeman regime. The transformation presents an interesting quantum-mechanical problem since the quantization axis changes from being aligned along the axis of the electric-field gradient tensor (the cell symmetry axis) to being aligned along the magnetic field. The large nuclear quadrupole shifts present in our system enable us to study this regime with relatively high resolution. We achieve large nuclear quadrupole shifts for I=3/2 131Xe by using a cube-shaped 1 mm3 vapor cell with walls of different materials. The enhancement of the NQR shift from the cell wall materials opens up a new parameter to tune to control the nuclear quadrupole interactions in vapor cells.

Any atom that has a nuclear spin I ≥ 1 has a nuclear electric quadrupole moment, whose interactions with electric field gradients can cause shifts of the nuclear magnetic energy levels. I=3/2 131Xe has four nuclear sublevels, and the resonance is split into a triplet at relatively high fields such that the Larmor frequency is higher than the NQR splitting. At low fields, the lines collapse into a singlet at the NQR frequency. We have measured multiple nuclear resonance spectra versus field magnitude for several field angles relative to the cell symmetry axis, ϕ. Data are presented in Fig. 1. The black lines show the transition frequencies for 129Xe versus magnetic field. Since 129Xe has no nuclear electric quadrupole moment (I=1/2), the transition energy is linear in applied field. The gray lines represent the energy differences between the four nuclear sublevels of 131Xe found numerically.

Contact: Elizabeth Donley

References:

E. A. Donley, J. L. Long, T. C. Liebisch, E. R. Hodby, T. A. Fisher, and J. Kitching, Nuclear Quadrupole Resonances in Compact Vapor Cells: The Crossover from the NMR to the NQR Interaction Regimes, Physical Review A 79, 013420 (2009)