NIST Optical Frequency Measurements Group


Quenched narrow-line cooling of neutral calcium

Photograph of the calcium optical clock experiment. Clearly seen are the red, green, and blue laser colors used in these experiments. Relevant calcium energy levels for quenched narrow-line laser cooling. Shown are the 657 nm clock/cooling transition from the 4s4s singlet ground state to the 4s4p triplet excited state; the 552 nm quenching transition from triplet 4s4p to the singlet 4s5s; the 1.03 micron decay route from 4s5s to 4s4p; and the final decay route from the 4s4p to the 4s4s ground state.

Overview

One of the biggest limitations for the calcium optical frequency standard based on atoms released from the blue MOT is the residual motion of the atoms associated with their 2 mK temperature.� These comparatively warm temperatures result from the fact the alkaline earth atoms like Ca have no ground-state magnetic substructure, thereby precluding any sub-Doppler cooling mechanisms.� Thus, one is left with pure Doppler cooling on a fairly broad transition (34 MHz for Ca).� From Doppler cooling theory it is well known that the transition linewidth sets the attainable cooling limit, which for the 423 nm transition is around 1 mK.� To reduce the temperature of the atoms further, a second stage of laser cooling is required.� One approach is to perform the cooling with a much narrower transition for which the cooling limit will be much lower.� Fortunately such a transition exists in the alkaline earths, namely the clock transition itself, from the ¹S₀ ground state to the ³P₁excited state.� For heavy alkaline earth atoms like Sr, the clock transition linewidth is ideal for second stage cooling and has achieved temperatures around 1 mK.� However, the clock transition in Ca is so narrow, that while it could in principle achieve very cold temperatures in laser cooling, it scatters photons too slowly to cool efficiently.� By adding a laser at 552 nm that connects the ³P₁ excited state to a higher-lying ¹S₀ state that quickly returns the atom to the ground state via ¹P₁(see the energy diagram above), we accelerate the cooling process to the point where it can efficiently cool the atoms.� This idea of “quenching” of the excited state to enable laser cooling on narrow transitions was first demonstrated in the context of sideband cooling of trapped ions.� In our calcium experiments, we have implemented quenched narrow-line cooling (QNLC) in several different ways.� In one dimension we have shown that by using shaped pulses in the time domain to produce the desired cooling frequency spectrum, we can cool the atoms to sub-mK temperatures using a step-wise quenching process.� In three dimensions these pulsed schemes become more complicated and it is more efficient instead to use continuous simultaneous illumination of the atoms with both the cooling and quenching lasers.� We have used simultaneous cooling to transfer more than 30% of the atoms from the 423 nm MOT to a magneto-optic trap based on 657 nm and 552 nm lasers, with resulting temperatures below 10 mK.� Similar results have been achieved with a different quenching transition by the calcium group at PTB in Braunschweig, Germany.� While these results are particular to calcium, we note that this technique has considerable generality and could be applied to any narrow transition such as the analogous transition in Mg.

Three dimensional quenched narrow line cooling

We constructed a QNLC magneto-optic trap by overlapping 657 nm cooling beams (4 mW per beam) with the 423 nm MOT laser beams in all three dimensions, while overlapping the 552 nm in two.� It is useful (although not necessary) to have the green light in as many dimensions as possible for two reasons.� First, by multi-passing a single laser beam, one can achieve a higher quenching rate for a given laser power, which is important since sufficient quenching on this weak intercombination line requires more than 50 mW in our present configuration (we typically use 90 mW).� Second, by configuring the green light to have a polarization opposite to that of the red, the absorbed quenching photons can actually assist the cooling by transferring momentum in the direction opposite to that of a given atom’s motion.� The quenching effectively broadens the cooling transition to about 10 kHz, but to transfer efficiently atoms from the blue MOT to the QNLC MOT, we need a capture range closer to 1 MHz.�� By frequency modulating the red laser at 20 kHz we generate a series of sidebands on the cooling laser spectrum over a 1 MHz span.� The highest frequency components of this span are detuned to the red by ~100 kHz to provide the proper sign for Doppler cooling.� The 552 nm light is provided by a dye laser whose frequency is fixed on the ³P₁→¹S₀ resonance by offset locking to a suitable I₂ transition.� Due to the narrow effective linewidth of the cooling transition, only a small magnetic quadrupole field (~200 mG/cm) is required to complete the magneto-optic trap.� It typically takes 6-10 ms for the atoms to reach near equilibrium conditions for our cooling parameters.� Longer cooling times achieve slightly lower temperatures at the expense of reduced atom number.� By scanning the frequency of a probe laser over resonance, we can map the atomic velocity distribution into the frequency domain via the Doppler shift.� The figure below shows the velocity distribution (in red) of the atoms after being released from the QNLC MOT.� For comparison, we show the distribution associated with the blue MOT: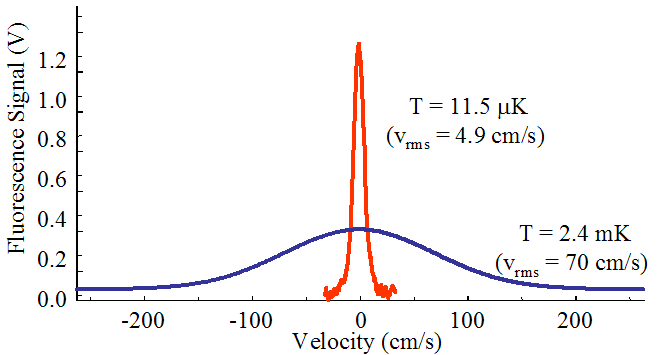

Velocity distributions showing the 2 millikelvin temperature achieved in the 423 nm MOT and the 10 microkelvin temperature achieved in the quenched narrow-line cooling MOT.

One dimensional third-stage quenched narrow-line cooling to sub-recoil temperatures

While continuous cooling with a frequency-modulated spectrum is certainly a straightforward way to cool atoms in three dimensions, we have also experimented with pulsed cooling, where one can have good control over the cooling spectrum.� These demonstrations have been performed in one dimension and have achieved sub-recoil temperatures for calcium.� We start with a sample of atoms that have been cooled in three dimensions to 10 mK using the method described in the previous section.� We then use cooling pulses of red light that are square in the time domain, and thus have a sinc² frequency spectrum (a similar approach was first demonstrated in Raman cooling of alkali 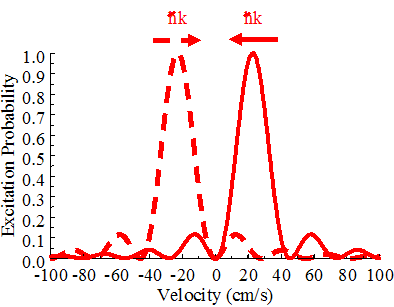elements by the group of Steve Chu).� By red detuning these pulses so that the first zero of the sinc² function is located on the atomic resonance (i.e. resonant with zero velocity atoms), we create a dark state around zero velocity.� Due to the red detuning of the cooling pulses, atoms are driven towards zero velocity (see figure below left) – if after subsequent spontaneous emission their velocity lands near zero, they have little chance of re-excitation since there is no resonant light present.� Through repetition of the cooling sequence (consisting of one red cooling pulse from each direction, followed by a 50 ms green quenching pulse to put the atoms back in the ground state), atoms accumulate around zero velocity.� Longer cooling pulses give a narrower spectrum allowing colder temperatures but have a smaller capture range.� We have experimented with various combinations of different pulse lengths.� 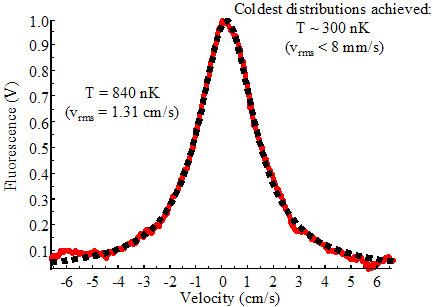A typical resulting velocity distribution is shown below right (data shown in red – the black dots show a best fit Lorentzian) with sub recoil width.� It is interesting that such a distribution could be achieved with only 1 ms of third stage cooling.

Schematic outlining the pulsed quenched narrow-line cooling technique. Excitation by sinc-squared frequency domain shapes drive atoms toward a zero-excitation region around zero velocity. Velocity distribution resulting from the cooling pulse sequence. Shown is a lorentzian shaped curve demonstrated sub-recoil cooling in one dimension for calcium. This corresponds to a temperature of 840 nK or a velocity of 1.31 cm/s. The coldest distribution achieved was ~ 300 nK.